Answer:
Below
Explanation:
Given Data:
- The sum of two numbers is less than 2
- If we subtract the second number from the first , the difference is greater than 1
Q) What are the two numbers?
Lets suppose the first number to be x and the second number to be y
The first point states sum of two number which is x + y is less than 2 so our first expression becomes,
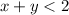
The second point states that the if we subtract the second number from the first number which states x - y the difference is greater than 1 so our second expression becomes,
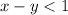
1) The riddle can be represented by a system of inequalities. Write an inequality for each statement.
The inequality for the first statement is
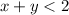
The inequality for the second statement is
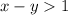
I assume the second part to the question would be solve for x and y xD
so here goes
2)
If we just simply add both the equations we get the following result:
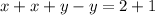
Just suppose there is an equal to sign instead of less than or greater than

now put the value of x in any one of the two equations I choose equation 1
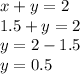
I attached an image so you can understand it better :)