Question

Which equation is non-linear?

A)
`y=3x^3-10`
B)
`y=1/2x+4`
C)
`y=4x-5/3`
D)
`-3x--7y=-21`

Answer 1

`\huge\boxed{\text{A is not linear.}}`

Explanation:

Linear equations are equations that, when graphed, form a "line" and have a constant rate of change.

Usually, these are in the form
`y=mx+b` when put in that order.

There are a few types of equations, I'll list some of the major ones

• Linear = has a constant rate of change
• Exponential = increases for x as the exponent
• Quadratic = is in a binomial, trinomial, or polynomial - it has a vertex

Linear functions are usually in the form
`y=mx+b`

Exponential functions are usually in the form
`y=b^x`

Quadratic functions are usually in the form
`ax^2 + bx + c`

We must note that linear functions can not

A) Have an exponent on any x term

B) Have x and y multiplied by each other

We can see that every equation, except A

A) Follows the form
`y=mx+b` (
`-3x--7y=-21` can be simplified to
`y= (3)/(7)x-3`)

B) Does not have any exponents on their x terms

That leaves A) to be the equation that isn't linear.

Hope this helped!

Answer 2

Equation A is non-linear.

Explanation:

We are given four equations in which we need to determine if they are linear or non-linear relationships.

Firstly, we need to know some information about linear equations:

• Linear equations cannot have an exponent.
• Linear equations have a constant slope and are straight lines.
• Linear equations can be negative or positive.
• Linear equations have a domain of all real numbers. They also have a range of all real numbers.

Now, in order to check this easily, we need to place these equations into slope-intercept form.

Equation A

`\displaystyle y = 3x^3 - 10`

We see that this has an exponent, so this cannot be a linear equation.

In fact, because it is cubed, this is called a cubic function. Therefore, equation A is not a linear equation.

Equation B

`\displaystyle y = (1)/(2)x + 4`

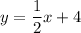
This equation does not have a exponent. It also has a slope and a y-intercept. Therefore, equation B is a linear equation.

Equation C

`\displaystyle y = 4x -(5)/(3)`

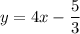
The equation does not have a exponent. It also has a slope and a y-intercept. Therefore, equation C is a linear equation.

Equation D

`-3x--7y = -21`

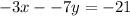
First off, we need to get this equation into slope-intercept form, if possible.

`\displaystyle -3x -- 7y = -21\\\\-3x + 7y = -21 \ \ \ \text{Change the sign on 7y.}\\\\7y = 3x - 21 \ \ \ \text{Move 3x to the other side by adding.}\\\\(7y)/(7)=(3x-21)/(7) \ \ \ \text{Divide both sides by 7 to isolate y.}\\\\\bold{y = (3)/(7)x-3}`

Our final equation is
`\displaystyle y = (3)/(7)x-3`.

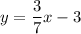The equation does not have an exponent. It has a constant slope and a y-intercept. Therefore, equation D is a linear equation.

Let's check our equations:

• Equation A:
  `\displaystyle y = 3x^3 - 10 \ \text{X}`
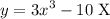
• Equation B:
  `\displaystyle y = (1)/(2)x + 4 \ \checkmark`
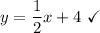
• Equation C:
  `\displaystyle y = 4x -(5)/(3) \ \checkmark`
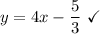
• Equation D:
  `\displaystyle y = (3)/(7)x-3 \ \checkmark`

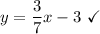
Therefore, we have determined that Equation A is not a linear equation, making it non-linear.