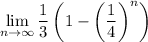Answer:
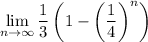
Explanation:
Series: the sum of the elements of a sequence.
Therefore, as the numbers have been defined as a series and we need to find
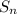 :
:
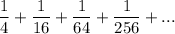
First determine if the sequence is arithmetic or geometric.
If it is an arithmetic sequence, there will be a common difference between consecutive terms.
if it is a geometric sequence, there will be a common ratio between consecutive terms.
From inspection of the terms, we can see that there is a common ratio of 1/4, as each term is the previous term multiplied by 1/4, so it is a geometric series.
Sum of the first n terms of a geometric series:
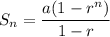
Given:
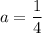
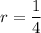
Substitute the values of a and r into the formula:



Therefore: