Question

How is a system of equations created when each linear function is given as a set of two ordered pairs. Explain

Answer 1

Sample response: Use the two points of a linear function to write an equation in slope-intercept form by first finding the slope of the function, and then using a point and the slope to determine the y-intercept. Write the equations in slope-intercept form.

Answer 2

Please check the explanation.

Explanation:

If each linear function is given as a set of two ordered pairs, all we need is to find a slope between two lines and put one of the points in the slope- intercept form of the line equation to find the y-intercept 'b' and then writing the equation in the slope-intercept form. This is how we can generate a system of equations.

For example, let suppose a linear function has the following ordered pairs:

• (1, 1)

• (2, 3)

Finding the slope between two points

`\left(x_1,\:y_1\right)=\left(1,\:1\right),\:\left(x_2,\:y_2\right)=\left(2,\:3\right)`

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`m=(3-1)/(2-1)`

`m=2`

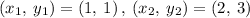
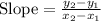
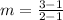
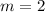
We know that the slope-intercept form of the line equation is

`y=mx+b`

where m is the slope and b is the y-intercept

Now, substituting the slope m = 2 and the point (1, 1) to determine the y-intercept

`y=mx+b`

`1 = 2(1)+b`

`b = 1-2`

`b = -1`

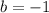
Now, substituting the slope m = 2 and the value of y-intercept in the slope-intercept form of the line equation

`y=mx+b`

`y=2x+(-1)`

`y=2x-1`

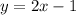
Thus, the equation of a line with the linear function having the points (1, 1) and (2, 3) is:

• 
  `y=2x-1`

This is how a system of equations created when each linear function is given as a set of two ordered pairs.