Answer:
Please check the explanation.
Explanation:
If each linear function is given as a set of two ordered pairs, all we need is to find a slope between two lines and put one of the points in the slope- intercept form of the line equation to find the y-intercept 'b' and then writing the equation in the slope-intercept form. This is how we can generate a system of equations.
For example, let suppose a linear function has the following ordered pairs:
Finding the slope between two points
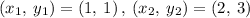
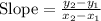
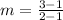
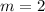
We know that the slope-intercept form of the line equation is
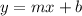
where m is the slope and b is the y-intercept
Now, substituting the slope m = 2 and the point (1, 1) to determine the y-intercept
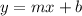
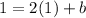
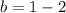
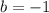
Now, substituting the slope m = 2 and the value of y-intercept in the slope-intercept form of the line equation
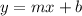
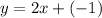
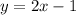
Thus, the equation of a line with the linear function having the points (1, 1) and (2, 3) is:
This is how a system of equations created when each linear function is given as a set of two ordered pairs.