Answer:
Inverse of
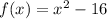 is
is

Option A is correct option.
Explanation:
We need to find inverse of
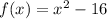
For finding inverse replace f(x) with y

Now, solve for x
Adding 16 on both sides

Taking square root on both sides:
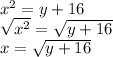
Now replace x with f^{-1}(x) and y with x

So, inverse of
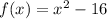 is
is

Option A is correct option.