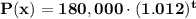Question

The population of a town has grown at a rate of approximately 1.2% each year since 1960. In 1960 the population of the town was about 180 thousand people. Which functions could be used to model the population,p, of the town (in thousand) x years after 1960?

Answer 1

To model the population of a town x years after 1960, an exponential function can be used.

Step-by-step explanation:

To model the population, p, of the town x years after 1960, we can use an exponential function. Since the population grows at a rate of approximately 1.2% each year, the formula for the exponential function would be:

`p = 180*(1+0.012)^x`

Where p is the population in thousands and x is the number of years after 1960. This formula takes the initial population of 180 thousand people in 1960 and multiplies it by the growth factor of (1+0.012) raised to the power of x.

Answer 2

`P(x)=180,000\cdot(1.012)^t`

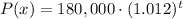
Step-by-step explanation:

Exponential Function

The exponential function is often used to model natural growing or decaying processes, where the change is proportional to the actual quantity.

An exponential growing function is expressed as:

`P(x)=P_o\cdot(1+r)^x`

Where:

P(t) is the actual value of the function at time t

Po is the initial value of P at x=0

r is the growth rate, expressed in decimal

We need to find the model for the population of a town that grows at a rate of r = 1.2% = 0.012 each year since 1960.

We are given the population in 1960 as Po=180,000 people. Using the variable x as the number of years since 1960:

`P(x)=180,000\cdot(1+0.012)^t`

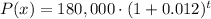
Operating:

`P(x)=180,000\cdot(1.012)^t`

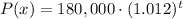
The function to model the population of the town is:

`\mathbf{P(x)=180,000\cdot(1.012)^t}`