Question

Which of the following inequalities matches the graph?

Answer 1

6x - y < 3

Explanation:

Finding the equation of the inequality :

Slope :

⇒ m = 3 - (-3) / 0 - (-1)

⇒ m = 6/1

⇒ m = 6

Y-intercept :

⇒ (0, 3)

Equation :

⇒ y = 6x + 3

Here :

⇒ Above the origin, so it is greater than ( > )

⇒ y > 6x + 3

⇒ 6x - y < 3

Answer 2

6x - y < -3

Explanation:

When graphing inequalities:

< or > = dashed line

≤ or ≥ = solid line

< or ≤ = shade below the line

> or ≥ = shade above the line

Create an equation for the line

Choose 2 points on the line:

• let (x₁, y₁) = (-1, -3)
• let (x₂, y₂) = (0, 3)

Calculate the slope:

`\sf \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(3-(-3))/(0-(-1))=6`

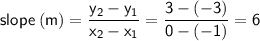
Determine the equation for the line using the point-slope formula:

`\implies\sf y-y_1=m(x-x_1)`

`\implies \sf y-(-3)=6(x-(-1))`

`\implies \sf y+3=6(x+1)`

`\implies \sf y=6x+3`

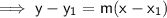
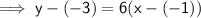
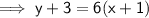
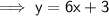
As the shading is above the line:

⇒ y > 6x + 3

Compare with answer options

Rearrange each answer option to make y the subject:

Option (a)

-6x + y < 3

⇒ y < 6x + 3

Option (b)

6x + y < 3

⇒ y < -6x + 3

Option (c)

6x - y < -3

⇒ -y < -6x - 3

⇒ y > 6x + 3

Therefore, as option C matches the calculated inequality, the answer is

6x - y < -3