Answer:
6x - y < -3
Explanation:
When graphing inequalities:
< or > = dashed line
≤ or ≥ = solid line
< or ≤ = shade below the line
> or ≥ = shade above the line
Create an equation for the line
Choose 2 points on the line:
- let (x₁, y₁) = (-1, -3)
- let (x₂, y₂) = (0, 3)
Calculate the slope:

Determine the equation for the line using the point-slope formula:
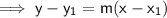
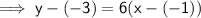

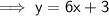
As the shading is above the line:
⇒ y > 6x + 3
Compare with answer options
Rearrange each answer option to make y the subject:
Option (a)
-6x + y < 3
⇒ y < 6x + 3
Option (b)
6x + y < 3
⇒ y < -6x + 3
Option (c)
6x - y < -3
⇒ -y < -6x - 3
⇒ y > 6x + 3
Therefore, as option C matches the calculated inequality, the answer is
6x - y < -3