Explanation:
First factor out the negative sign from the expression and reorder the terms
That's
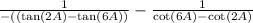
Using trigonometric identities
That's
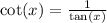
Rewrite the expression
That's
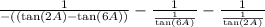
We have
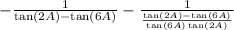
Rewrite the second fraction
That's
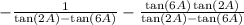
Since they have the same denominator we can write the fraction as
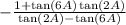
Using the identity

Rewrite the expression
We have
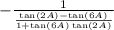
Using the trigonometric identity
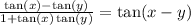
Rewrite the expression
That's

Which is
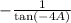
Using the trigonometric identity
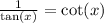
Rewrite the expression
That's
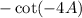
Simplify the expression using symmetry of trigonometric functions
That's
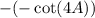
Remove the parenthesis
We have the final answer as

As proven
Hope this helps you