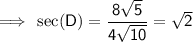Answer:

Explanation:
First, find the length of the hypotenuse using Pythagoras' Theorem:

(where a and b are the legs, and c is the hypotenuse, of a right triangle)
Given:
Subtituting the given values into the formula and solving for c:
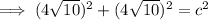

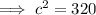
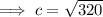
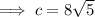
Therefore, the hypotenuse is
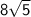
Secant of an angle in a right triangle:
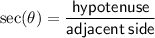
Given:
 = D
= D- hypotenuse =
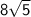
- adjacent side =

Substituting the given values into the formula: