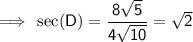Question

Help me with a explanation please!!

Answer 1

`\sf{\Large{\bold{\orange{The \: value \: of \: \sec (D) \: is \: √(2) }}}}`

Explanation:

`\textsf{\large{\underline{\green{To find:-}}}}`

The value of Sec(D)

`\textsf{\large{\underline{\blue{Given :-}}}}`

Perpendicular (P) = BC = 4√10

Base (B) = BD = 4√10

`\textsf{\huge{\underline{\underline{\pink{Solution :-}}}}}`

First of all we have to find length of DC to get hypotenuse

To find we will use Pythagoras theorem

`\sf {(hypotenuse)}^(2) = {(perpendicular)}^(2) + {(base)}^(2) \\ \sf {H}^(2) = {P}^(2) + {B}^(2)`

Now we will put the values of Perpendicular and base

`\sf {H}^(2) = {(4 √(10) )}^(2) + {(4 √(10) )}^(2) \\ \sf {H}^(2) = (16 * 10) + (16 * 10) \\ \sf {H}^(2) = 160 + 160 \\ \sf {H}^(2) = 320 \\ \sf H = √(320) \\ \sf H = 8 √(5)`

Hypotenuse (H) = CD = 8√5

Now we will put Sec formula

to find Sec(D)

`\sf \sec(D) = (hypotenuse)/(base) = (H)/(B) \\ \implies (8 √(5) )/(4 √(10) ) \\ \implies (2 √(5) )/( √(10) ) \\ \implies (2 √(5) )/( √(2) √(5) ) \\ \implies (2)/( √(2) ) \\ \implies{ \sf {\purple {√(2) }}}`

Answer 2

`\sf sec(D)=√(2)`

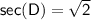
Explanation:

First, find the length of the hypotenuse using Pythagoras' Theorem:

`a^2+b^2=c^2`

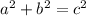
(where a and b are the legs, and c is the hypotenuse, of a right triangle)

Given:

• 
  `a=4√(10)`
• 
  `b=4√(10)`

Subtituting the given values into the formula and solving for c:

`\implies (4√(10))^2+(4√(10))^2=c^2`

`\implies 160+160=c^2`

`\implies c^2=320`

`\implies c=√(320)`

`\implies c=8√(5)`

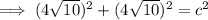
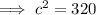
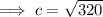
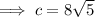
Therefore, the hypotenuse is
`\sf 8√(5)`

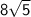
Secant of an angle in a right triangle:

`\sf \sec(\theta)=(\sf hypotenuse)/(\sf adjacent\:side)`

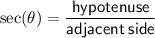
Given:

• 
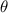  `\theta` = D
• hypotenuse =
  `\sf 8√(5)`
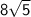
• adjacent side =
  `\sf 4√(10)`

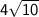
Substituting the given values into the formula:

`\implies \sf \sec(D)=(8√(5))/(4√(10))=\sqrt2}`