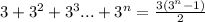For n prove by 3 + 3 {}^(2) + 3 {}^(3) ... + 3 {}^(n) = \frac{3(3 {}^(n) - 1) }{2} thank you​

Question

For n prove by


`3 + 3 {}^(2) + 3 {}^(3) ... + 3 {}^(n) = \frac{3(3 {}^(n) - 1) }{2}`
thank you​

Answer 1

12 5 that is the answer for your question

Answer 2

`3 + 3^2 + 3^3 ...+ 3^n = (3(3^n - 1))/(2)`

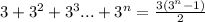
Explanation:

Given

`3 + 3^2 + 3^3 ...+ 3^n`

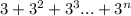
Required

Show that the sum of the series is
`(3(3^(n)-1))/(2)`

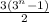
The above shows the sum of a geometric series and this will be calculated as shown below;

`S_n = (a(r^n - 1))/(r - 1)`

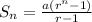
Where

a = First term;

`a = 3`

r = common ratio

`r = (3^2)/(3) = (3^3)/(3^2)`

`r = 3`

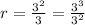
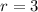
Substitute 3 for r and 3 for a in the formula above;

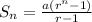`S_n = (a(r^n - 1))/(r - 1)` becomes

`S_n = (3(3^n - 1))/(3 - 1)`

`S_n = (3(3^n - 1))/(2)`

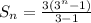
Hence;

`3 + 3^2 + 3^3 ...+ 3^n = (3(3^n - 1))/(2)`