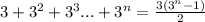Answer:
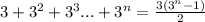
Explanation:
Given
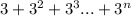
Required
Show that the sum of the series is
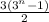
The above shows the sum of a geometric series and this will be calculated as shown below;
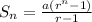
Where
a = First term;
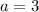
r = common ratio
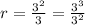
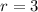
Substitute 3 for r and 3 for a in the formula above;
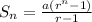 becomes
becomes
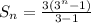
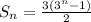
Hence;