Question

a random sample of n=24 data from a normal distribution with unkown variance produced x=42.5 and s=26 what is the 95 confidence interval

Answer 1

a

Explanation:

edge

Answer 2

95% of confidence intervals are

(31.5215 , 53.4785)

Explanation:

Explanation:-

Given sample size 'n' =24

Mean of the sample x⁻ = 42.5

Standard deviation of the sample 'S' = 26

95% of confidence intervals are determined by

`(x^(-) - t_(0.05) (S)/(√(n) ) , x^(-) + t_(0.05) (S)/(√(n) ))`

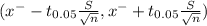
Degrees of freedom

ν =n-1 = 24-1 =23

`t_(0.05) = 2.0686`

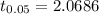
95% of confidence intervals are

`(42.5 - 2.0686 (26)/(√(24) ) , 42.5+ 2.0686 (26)/(√(24) ))`

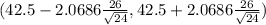
( 42.5 -10.9785 ,42.5 +10.9785)

(31.5215 , 53.4785)