Answer:
95% of confidence intervals are
(31.5215 , 53.4785)
Explanation:
Explanation:-
Given sample size 'n' =24
Mean of the sample x⁻ = 42.5
Standard deviation of the sample 'S' = 26
95% of confidence intervals are determined by
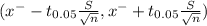
Degrees of freedom
ν =n-1 = 24-1 =23
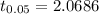
95% of confidence intervals are
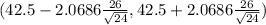
( 42.5 -10.9785 ,42.5 +10.9785)
(31.5215 , 53.4785)