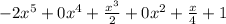Answer:
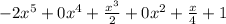
Explanation:
Given
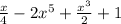
Required
The standard form of the polynomial
The general form of a polynomial is
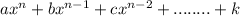
Where k is a constant and the terms are arranged from biggest to smallest exponents
We start by rearranging the given polynomial
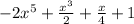
Given that the highest exponent of x is 5;
Let n = 5
Then we fix in the missing terms in terms of n
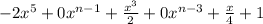
Substitute 5 for n
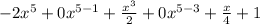
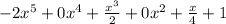
Hence, the standard form of the given polynomial is