Question

Please help, thank you

Answer 1

The sum = 4092

Explanation:

The sum is equal to A, in which:

A = 4 x (2^0 + 2^1 + 2^2 + ... + 2^9)

= 4 x [(1 + 2^1 + 2^2 + ... + 2^9)(2 - 1)/(2 - 1)]

= 4 x (2^10 - 1)(2 - 1)

= 4 x (2^10 - 1)

= 4 x 1023

= 4092

Hope this helps!

Answer 2

4092

Explanation:

The n th term of a geometric sequence is

`a_(n)` = a
`r^(n-1)`

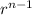
where a is the first term and r the common ratio

4
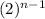`(2)^(n-1)` ← is the n th term of a geometric sequence

with a = 4 and r = 2

The sum to n terms of a geometric sequence is

`S_(n)` =
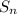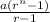`(a(r^(n)-1) )/(r-1)` , thus

`S_(10)` =
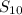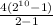`(4(2^(10)-1) )/(2-1)` = 4(1024 - 1) = 4 × 1023 = 4092