(A) The speed of the sphere of 27 kg is
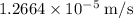 .
.
(B) The speed of sphere of mass 107 kg is
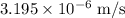 .
.
(C) The magnitude of the relative velocity with which one sphere is approaching to the other is
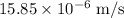 .
.
(D) The distance from the initial position of the center of the 27.0 sphere is 20.506 m.
Given data:
The mass of sphere 1 is,
 .
.
The mass of sphere 2 is,
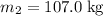 .
.
The radius of each spheres are, r = 0.10 m.
The distance between the centers of each sphere is, d = 41.0 m.
(A)
In this part, we can apply the conservation of energy to find the speed at given distance of 26.0 m. So,
Total energy at initial = Total energy at final
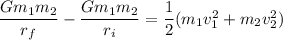
Now, as per the conservation of momentum,
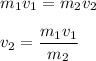
Therefore,
![(Gm_(1)m_(2))/(r_(f))-(Gm_(1)m_(2))/(r_(i))=(1)/(2)(m_(1)v^(2)_(1)+m_(2) * [m_(1)v_(1)/m_(2)]^(2))\\\\\\(Gm_(1)m_(2))/(r_(f))-(Gm_(1)m_(2))/(r_(i))=(m_(1)v^(2)_(1))/(2) * ((m_(1)+m_(2))/(m_(2)))](https://img.qammunity.org/2021/formulas/physics/college/cdk4xi7evea3sxw5uk0d19x34onu1t16lt.png)
Modifying as,
![v^(2)_(1)=[(2Gm^(2)_(2))/(m_(1)+m_(2))] * [(1)/(r_(f))-(1)/(r_(i))]](https://img.qammunity.org/2021/formulas/physics/college/3zsy4cjcdl9316nlrry963v56cbqk88hz5.png)
Substitute the values in the above result
![v^(2)_(1)=[(2 * 6.67 * 10^(-11) * 107^(2))/(27+107)] * [(1)/(26)-(1)/(41)]\\\\v_(1)=\sqrt{1.6038 * 10^(-5)}\\\\v_(1)=1.2664 * 10^(-5) \;\rm m/s](https://img.qammunity.org/2021/formulas/physics/college/sj8y6m6kl1xo4qixsm4igta9hnb8lmdgg4.png)
Thus, the speed of the sphere of 27 kg is
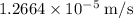 .
.
(B)
The sphere with mass 107 kg is calculated as,
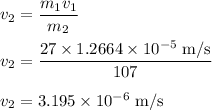
Thus, the speed of sphere of mass 107 kg is
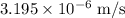 .
.
(C)
The magnitude of the relative velocity with which one sphere is
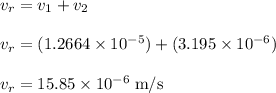
Thus, the magnitude of the relative velocity with which one sphere is approaching to the other is
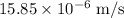 .
.
(D)
The distance of the centre is proportional to the acceleration,
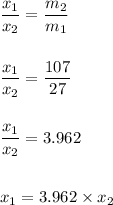
As per the given problem,
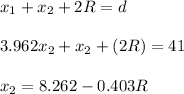
And,
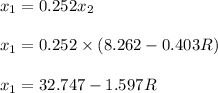
Then for point of contact of the sphere:
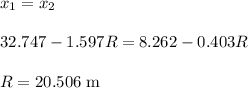
Thus, the distance from the initial position of the center of the 27.0 sphere is 20.506 m.
Learn more about the conservation of linear momentum here:
from the initial position of the center of the 27.0 sphere