Question

N experiment is performed in deep space with two uniform spheres, one with mass 27.0 and the other with mass 107.0 . They have equal radii, = 0.10 . The spheres are released from rest with their centers a distance 41.0 apart. They accelerate toward each other because of their mutual gravitational attraction. You can ignore all gravitational forces other than that between the two spheres.

A) When their centers are a distance 26.0 apart, find the speed of the 27.0 sphere.

B) Find the speed of the sphere with mass 107.0 .

C) Find the magnitude of the relative velocity with which one sphere is approaching to the other.

D) How far from the initial position of the center of the 27.0 sphere do the surfaces of the two spheres collide?

Answer 1

Step-by-step explanation:

Apply the law of conservation of energy

`KE_i+PE_i=KE_f+PE_f`

`Gm_1m_2[(1)/(r_f) -(1)/(r_1) ]=(1)/(2) (m_1v_1^2+m_2v_2^2)`

from the law of conservation of the linear momentum

`m_1v_1=m_2v_2`

Therefore,

`Gm_1m_2[(1)/(r_f) -(1)/(r_1) ]=(1)/(2) (m_1v_1^2+m_2v_2^2)`

`=(1)/(2) [m_1v_1^2+m_2[(m_1v_1)/(m_2) ]^2]\\\\=(1)/(2) [m_1v_1^2+(m_1^2v_1^2)/(m_2) ]\\\\=(m_1v_1^2)/(2) [(m_1+m_2)/(m_2) ]`

`v_1^2=[(2Gm_2^2)/(m_1+m_2) ][(1)/(r_f) -(1)/(r_1) ]`

Substitute the values in the above result

`v_1^2=[(2Gm_2^2)/(m_1+m_2) ][(1)/(r_f) -(1)/(r_1) ]`

`=[(2(6.67* 10^-^1^1)(107)^2)/(27+107) ][(1)/(26) -(1)/(41)] \\\\=1.6038* 10^-^1^0\\\\v_1=√(1.6038* 106-^1^0) \\\\=1.2664 * 10^-^5m/s`

B) the speed of the sphere with mass 107.0 kg is

`v_2=(m_1v_1)/(m_2)`

`=[(27)/(107) ](1.2664 * 10^-^5)\\\\=3.195* 10^-^6m/s`

C) the magnitude of the relative velocity with which one sphere is

`v_r=v_1+v_2\\\\=1.2664* 10^-^5+3.195*10^-^6\\\\=15.859*10^-^6m/s`

D) the distance of the centre is proportional to the acceleration

`(x_1)/(x_2) =(a_1)/(a_2) \\\\=(m_2)/(m_1) \\\\=3.962`

Thus,

`x_1=3.962x_2`

and

`x_2=0.252x_1`

When the sphere make contact with eachother

Therefore,

`x_1+x_2+2r=41\\x_1+0,252x_1+2r=41\\1.252x_1+2r=41\\x_1=32.747-1.597r`

And

`x_1+x_2+2r=41\\3.962x_2+x_2+2r+41\\4.962x_2+2r=41\\x_2=8.262-0.403r`

The point of contact of the sphere is

`32.747-1.597r=8.262-0.403r\\\\r=(24.485)/(1.194) \\\\=20.506m`

Answer 2

(A) The speed of the sphere of 27 kg is
`1.2664 * 10^(-5) \;\rm m/s`.

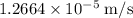(B) The speed of sphere of mass 107 kg is
`3.195 * 10^(-6) \;\rm m/s`.

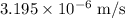(C) The magnitude of the relative velocity with which one sphere is approaching to the other is
`15.85 * 10^(-6) \;\rm m/s`.

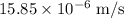(D) The distance from the initial position of the center of the 27.0 sphere is 20.506 m.

Given data:

The mass of sphere 1 is,
`m_(1) = 27.0 \;\rm kg`.

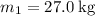The mass of sphere 2 is,
`m_(2) = 107.0 \;\rm kg`.

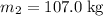The radius of each spheres are, r = 0.10 m.

The distance between the centers of each sphere is, d = 41.0 m.

(A)

In this part, we can apply the conservation of energy to find the speed at given distance of 26.0 m. So,

Total energy at initial = Total energy at final

`(Gm_(1)m_(2))/(r_(f))-(Gm_(1)m_(2))/(r_(i))=(1)/(2)(m_(1)v^(2)_(1)+m_(2)v^(2)_(2))`

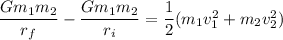
Now, as per the conservation of momentum,

`m_(1)v_(1)=m_(2)v_(2)\\\\v_(2)=(m_(1)v_(1))/(m_(2))`

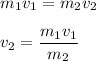
Therefore,

`(Gm_(1)m_(2))/(r_(f))-(Gm_(1)m_(2))/(r_(i))=(1)/(2)(m_(1)v^(2)_(1)+m_(2) * [m_(1)v_(1)/m_(2)]^(2))\\\\\\(Gm_(1)m_(2))/(r_(f))-(Gm_(1)m_(2))/(r_(i))=(m_(1)v^(2)_(1))/(2) * ((m_(1)+m_(2))/(m_(2)))`

Modifying as,

`v^(2)_(1)=[(2Gm^(2)_(2))/(m_(1)+m_(2))] * [(1)/(r_(f))-(1)/(r_(i))]`

Substitute the values in the above result

`v^(2)_(1)=[(2 * 6.67 * 10^(-11) * 107^(2))/(27+107)] * [(1)/(26)-(1)/(41)]\\\\v_(1)=\sqrt{1.6038 * 10^(-5)}\\\\v_(1)=1.2664 * 10^(-5) \;\rm m/s`

Thus, the speed of the sphere of 27 kg is
`1.2664 * 10^(-5) \;\rm m/s`.

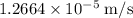(B)

The sphere with mass 107 kg is calculated as,

`v_(2)=(m_(1)v_(1))/(m_(2))\\\\v_(2)=(27 * 1.2664 * 10^(-5) \;\rm m/s )/(107)\\\\v_(2)=3.195 * 10^(-6) \;\rm m/s`

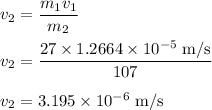
Thus, the speed of sphere of mass 107 kg is
`3.195 * 10^(-6) \;\rm m/s`.

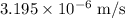(C)

The magnitude of the relative velocity with which one sphere is

`v_(r) = v_(1) +v_(2)\\\\v_(r) =( 1.2664 * 10^(-5))+ (3.195 * 10^(-6))\\\\v_(r)=15.85 * 10^(-6) \;\rm m/s`

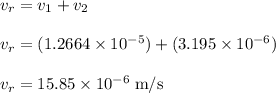
Thus, the magnitude of the relative velocity with which one sphere is approaching to the other is
`15.85 * 10^(-6) \;\rm m/s`.

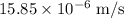(D)

The distance of the centre is proportional to the acceleration,

`(x_(1))/(x_(2))=(m_(2))/(m_(1))\\\\\\(x_(1))/(x_(2))=(107)/(27)\\\\\\(x_(1))/(x_(2))=3.962\\\\\\x_(1)=3.962 * x_(2)`

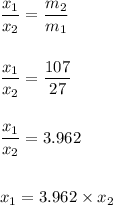
As per the given problem,

`x_(1)+x_(2)+2R = d\\\\3.962x_(2)+x_(2)+(2R) = 41 \\\\x_(2) = 8.262-0.403R`

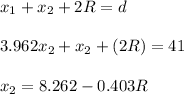
And,

`x_(1)=0.252x_(2)\\\\x_(1)=0.252 * (8.262-0.403R)\\\\x_(1)=32.747-1.597R`

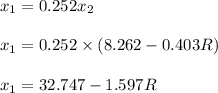
Then for point of contact of the sphere:

`x_(1) = x_(2)\\\\32.747-1.597R = 8.262-0.403R\\\\R =20.506 \;\rm m`

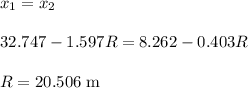
Thus, the distance from the initial position of the center of the 27.0 sphere is 20.506 m.

Learn more about the conservation of linear momentum here:

from the initial position of the center of the 27.0 sphere