Find the volume of the cone

Question

asked Dec 15, 2021 159k views

2 Answers

Pete Karl II · Answer 1 · 2021-12-16T00:20:01+0000

Answer:

12
$\pi$ units^3

Explanation:

V=1/3Bh

=1/3 Area of the base times height

Area of base:
$\pi$ r^2=4
$\pi$

height=9

4
$\pi$ times 9=36
$\pi$

1/3 of 36
$\pi$ =12
$\pi$

Lurline · Answer 2 · 2021-12-22T00:34:26+0000

Answer:

The volume of cone is
$\boxed{\tt{37.68}}$ units³.

Step-by-step explanation:

As per given question we have provided :

Here's the required formula to find the volume of cone :

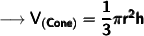
${\longrightarrow{\pmb{\sf{V_((Cone)) = (1)/(3)\pi{r}^(2)h}}}}$

Substituting all the given values in the formula to find the volume of cone :

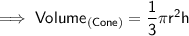
${\implies{\sf{Volume_((Cone)) = (1)/(3)\pi{r}^(2)h}}}$

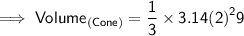
${\implies{\sf{Volume_((Cone)) = (1)/(3) * 3.14{(2)}^(2)9}}}$

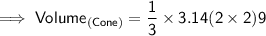
${\implies{\sf{Volume_((Cone)) = (1)/(3) * 3.14{(2 * 2)}9}}}$

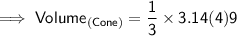
${\implies{\sf{Volume_((Cone)) = (1)/(3) * 3.14{(4)}9}}}$

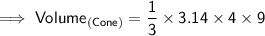
${\implies{\sf{Volume_((Cone)) = (1)/(3) * 3.14 * 4 * 9}}}$

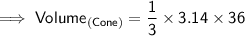
${\implies{\sf{Volume_((Cone)) = (1)/(3) * 3.14 * 36}}}$

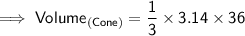
${\implies{\sf{Volume_((Cone)) = \frac{1}{\cancel{3}}* 3.14 * \cancel{36}}}}$

${\implies{\sf{Volume_((Cone)) = 3.14 * 12}}}$

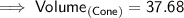
${\implies{\sf{Volume_((Cone)) = 37.68}}}$

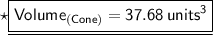
$\star{\underline{\boxed{\sf{\red{Volume_((Cone)) = 37.68 \: {units}^(3)}}}}}$

Hence, the volume of cone is 37.68 units³.

$\rule{300}{2.5}$