Question

Using function notation, describe the transformation. x^2+y^2=1 --> (x-7)^2 + (y+4)^2 = 1

PLEASE HELP!!!

Answer 1

f(x - 7) - 4

Translation: < 7 , -4 >

Explanation:

x^2+y^2=1

Centre: (0,0)

(x-7)^2 + (y+4)^2 = 1

Centre: (7,-4)

Translation: < 7 , -4 >

If the first function is f(x), the transformed function is:

f(x - 7) - 4

Answer 2

Explanation:

Step 1: Describe the transformation

The formula of transformation for this equation is
`(x - k)^2 + (y - b)^2 = 1`

If k or b has a positive sign in the formula, that means that the you move it to the negative direction. If k or b has a negative sign in the formula, that means that you move it to the positive direction.

So if we have
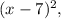`(x - 7)^2,` that means we move the x value to the positive direction 7 units.

So if we have
`(y + 4)^2`, that means we move the y value to the negative direction 4 units.

Answer: To the right 7 units and down 4 units.