Explanation:
Step 1: Describe the transformation
The formula of transformation for this equation is
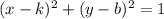
If k or b has a positive sign in the formula, that means that the you move it to the negative direction. If k or b has a negative sign in the formula, that means that you move it to the positive direction.
So if we have
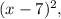 that means we move the x value to the positive direction 7 units.
that means we move the x value to the positive direction 7 units.
So if we have
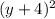 , that means we move the y value to the negative direction 4 units.
, that means we move the y value to the negative direction 4 units.
Answer: To the right 7 units and down 4 units.