Question

Alfonso graphs the inequality x greater-than negative 8 using the steps below.

Step 1: Draw a number line, and place an open circle at –8.
A number line going from negative 13 to negative 3. An open circle is at negative 8.
Step 2: Shade to the left of –8 to represent the infinite solutions to x greater-than negative 8.
A number line going from negative 13 to negative 3. An open circle is at negative 8. Everything to the left of the circle is shaded.
Step 3: Check work by substitution.
x = negative 9
Negative 9 greater-than negative 8 False

Which best describes the situation?
i know its kinda hard
A-The graph is incorrect. He should have used a closed circle at –8.
B-The graph is incorrect. He should have shaded to the right of –8.
C-The graph is correct. He should have checked his work with a number that was not on the shaded portion of the graph.
D-The graph is correct. He should have checked his work using –8.

Answer 1

I got the answer B too.

Explanation:

All you have to do is re read your question

HOPE THIS HELPS:)

STAY SAFE

Answer 2

B-The graph is incorrect. He should have shaded to the right of –8.

Explanation:

We examine the steps Alfonso follows in graphing the inequality x > -8.

Step 1: Draw a number line, and place an open circle at –8.

A number line going from negative 13 to negative 3. An open circle is at negative 8.

The first step is correct, since we use an open circle for > or < and a closed circle for
`\leq \:or\: \geq`.

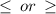Step 2: Shade to the left of –8 to represent the infinite solutions to x greater-than negative 8.

This step is incorrect since values to the left are always less than.

He should have shaded to the right of -8.

The error made is Option B.

CHECK:

x=-7

-7>-8 (TRUE)