Answer:
10cm
Explanation:
Given a cone of base radius r and slant height l, the Lateral Area (Curved Surface Area) of the cone is determined using the formula:
Lateral Area of a Cone =
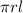
Diameter of the Cone = 24cm
Radius = Diameter/2 =24/2 =12 cm
Therefore:
Lateral Area of a Cone =
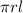

Therefore, the slant height of the cone is 10cm