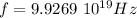Answer:
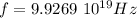
Step-by-step explanation:
Recall that the velocity (v) of a light wave is defined as the product of its frequency (f) times its wavelength (
 ) :
) :
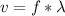
therefore, we can solve for the unknown frequency by dividing both sides of the equation by the frequency:
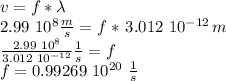
Since the units "1/second" are what we call Hertz (Hz), the answer can also be given as: