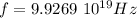Question

It is determined that a certain light wave has a wavelength of 3.012 ×10−12 m. The light travels at 2.99 ×108 m/s. What is the frequency of the light wave? (Round your answer to three significant figures.)

Answer 1

f=9.93 × 1019 Hz

Step-by-step explanation:

Use the relationship f=vλ to solve for frequency f. Substituting the known quantities yields:

f=vλf=2.99 × 108 m/s3.012 × 10-12 mf=9.926×1019

answer rounded off to 3 significant digits is

f=9.93 × 1019 Hz

Answer 2

`f=9.9269\,\,10^(19) Hz`

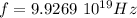
Step-by-step explanation:

Recall that the velocity (v) of a light wave is defined as the product of its frequency (f) times its wavelength (
`\lambda`) :

`v=f*\lambda`

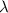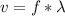
therefore, we can solve for the unknown frequency by dividing both sides of the equation by the frequency:

`v=f*\lambda\\2.99\,\,10^(8) (m)/(s) = f *\,3.012\,\,10^(-12)\, m\\(2.99\,\,10^8)/(3.012\,\,10^(-12)) (1)/(s)=f\\ f=0.99269\,\,10^(20)\,\, (1)/(s)\\`

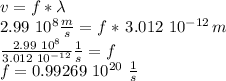
Since the units "1/second" are what we call Hertz (Hz), the answer can also be given as:

`f=9.9269\,\,10^(19) Hz\,`