Question

F(x)=x-1/x^2-x-6 which is the graph of

Answer 1

Answer: The first one is the answer

Explanation:

Answer 2

The graph is attached below.

Explanation:

As you have not added the graph, so I will be solving the function for a graph.

Given the function

`f\left(x\right)=x-(1)/(x^2)-x-6`

`x-\mathrm{axis\:interception\:points\:of\:}-(1)/(x^2)-6:`

`\mathrm{x-intercept\:is\:a\:point\:on\:the\:graph\:where\:}y=0`

`-(1)/(x^2)-6=0`

`-1-6x^2=0`

`\mathrm{No\:Solution\:for}\:x\in \mathbb{R}`

`\mathrm{No\:x-axis\:interception\:points}`

`y-\mathrm{axis\:interception\:point\:of\:}-(1)/(x^2)-6:`

`y\mathrm{-intercept\:is\:the\:point\:on\:the\:graph\:where\:}x=0`

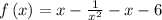
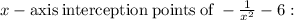
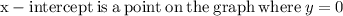
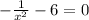
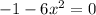
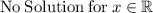
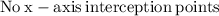
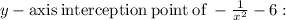
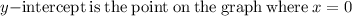
As we know that the domain of a function is the set of input or argument values for which the function is real and defined.

`\mathrm{Domain\:of\:}\:-(1)/(x^2)-6\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<0\quad \mathrm{or}\quad \:x>0\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:0\right)\cup \left(0,\:\infty \:\right)\end{bmatrix}`

`\mathrm{Since}\:x=0\:\mathrm{is\:not\:in\:domain}`

`\mathrm{No\:y-axis\:interception\:point}`

`\mathrm{Asymptotes\:of}\:-(1)/(x^2)-6:\quad \mathrm{Vertical}:\:x=0,\:\mathrm{Horizontal}:\:y=-6`

`\mathrm{Range\:of\:}-(1)/(x^2)-6:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)<-6\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-6\right)\end{bmatrix}`

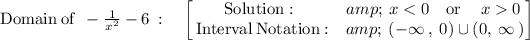
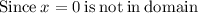
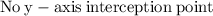
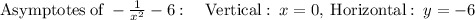
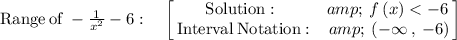
The graph is attached below.