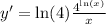Answer:
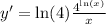
Explanation:
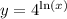
Take natural log of both sides:
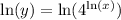
Use power rule of logarithms:
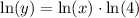
Let's differentiate.
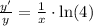
I applied chain rule on the left side and I apply constant multiple rule to the right side.
Let's multiply both sides by
 :
:
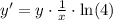
We started with
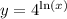 so let's make that replacement:
so let's make that replacement:
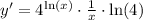
Let's simplify it a bit: