Answer:
24 square units
Explanation:
The area of a polygon can be computed from its list of coordinates as ...
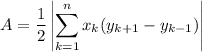
where there are n coordinate points. Subscripts on y "wrap around" so that ...

The area from these coordinates is ...
A = (1/2)|-2(-2-1) +4(1-(-2)) +5(3-(-2)) +2(1-1) -1(-2-3)|
= (1/2)|6 +12 +25 +0 +5|
= (1/2)(48)
= 24 . . . . square units
_____
If you graph the points, you see that the figure can be considered to be a parallelogram topped by a triangle. The area of the parallelogram is ...
A = bh = 6·3 = 18
The area of the triangle is ...
A = 1/2bh = (1/2)(6)(2) = 6
Then the total area is 18+6 = 24, which agrees with the above calculation.