Answer:
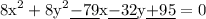
Explanation:
we are given 3 points which lie in a circle of the circle equation we want to figure out missing constant and coefficients
our given equation
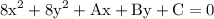
to figure out the missing coefficients and the constant we can consider system of equation because we have three points by using the points we can create the system of equations from the first point we obtain:
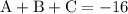
from the second point we acquire:
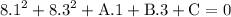
simplify:
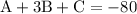
from the third point we get:
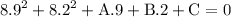
simplify:
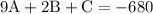
therefore our system of equations is:
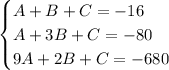
by solving the equation we acquire:
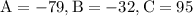
substitute hence, our equation is
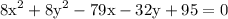
and we are done!