Question

URGENT!! NEED THIS IN TWO HOURS. DUMB ANSWERS WILL BE REPORTED ALTHOUGH I UNDERSTAND IF YOU MAKE A SIMPLE MISTAKE IN YOUR CALCULATIONS. I NEED THE FULL ANSWER AND EXPLANATION BELOW

Write the general equation for the circle that passes through the points (1, 1), (1, 3), and (9, 2).



You must include the appropriate sign (+ or -) in your answer. Do not use spaces in your answer.

8x^2 + 8y^2 _____x _______y _______= 0
ANSWERS MUST BE A ROUND NUMBER

Answer 1

Yo sup??

The given points are (1,1),(1,3) and (9,2)

equation of circle is

8x²+8y²+ax+by=0

let us plug in (1,1) in the equation we get

8+8+a+b=0

a+b=-16

let us now plug in (1,3) in the equation

8+8*3²+a+3b=0

a+3b=-80

let us. now solve the two equation in terms of a and b

we get

2b=--64

b=-32

and

a=-16+32

=16

therefore the equation is

8x²+8y²+16x-32y=0

Hope this helps

Answer 2

`\rm \displaystyle 8{x}^(2) + 8{y}^(2) \underline{- 79}x \underline{ - 32}y \underline{ + 95 }= 0`

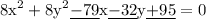
Explanation:

we are given 3 points which lie in a circle of the circle equation we want to figure out missing constant and coefficients

our given equation

`\rm \displaystyle 8{x}^(2) + 8{y}^(2) + Ax + By + C = 0`

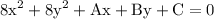
to figure out the missing coefficients and the constant we can consider system of equation because we have three points by using the points we can create the system of equations from the first point we obtain:

`\rm \displaystyle A + B+ C = - 16`

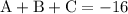
from the second point we acquire:

`\rm \displaystyle 8{.1}^(2) + 8{.3}^(2) + A.1+ B.3+ C = 0`

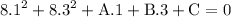
simplify:

`\rm \displaystyle A+ 3B+ C = - 80`

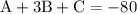
from the third point we get:

`\rm \displaystyle 8{.9}^(2) + 8{.2}^(2) + A.9 + B.2 + C = 0`

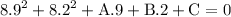
simplify:

`\rm \displaystyle 9 A+ 2B + C= - 680`

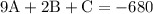
therefore our system of equations is:

`\begin{cases}A + B + C = - 16 \\A + 3B + C = - 80 \\9A + 2B + C = - 680\end{cases}`

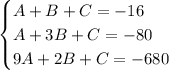
by solving the equation we acquire:

`\displaystyle \rm A = - 79,B = - 32,C = 95`

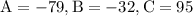
substitute hence, our equation is

`\rm \displaystyle 8{x}^(2) + 8{y}^(2) - 79x - 32y + 95 = 0`

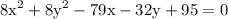
and we are done!