Answer:
Part a:
The hypothesis are
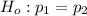 and
and
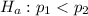 .
.
Part b:
The Type I error is when the null hypothesis is true but is rejected wrongly. In this case this would indicate that there was no discrimination, but it was wrongly rejected and thus the company is defamed for gender discrimination.
Type II error is when a false null hypothesis is accepted. In this case this would mean that there was a discrimination in the process of hiring but the company is not made accountable for the issue.
Part c:
When the value of alpha is taken as 1% the probability of committing type II error is reduced.
Part d:
When sample size is increased to 1000 employees the probability of committing type II error is reduced further.
Explanation:
As the probability of the women being employed is given as p1 and the probability of the man being employed is given as p2.
Part A
The hypotheses are as follows
The null hypothesis indicate that there is no difference between the probabilities of woman being employed or man being employed. So
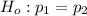
The alternative hypothesis describes that the probability of women employment is less than that of men being employed thus
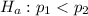
Part B
The Type I error is when the null hypothesis is true but is rejected wrongly. In this case this would indicate that there was no discrimination, but it was wrongly rejected and thus the company is defamed for gender discrimination.
Type II error is when a false null hypothesis is accepted. In this case this would mean that there was a discrimination in the process of hiring but the company is not made accountable for the issue.
Part C
Higher values of α make it easier to reject the null hypothesis, so choosing higher values for α can reduce the probability of a Type II error.
The consequence here is that if the null hypothesis is true, increasing α makes it more likely that we commit a Type I error (rejecting a true null hypothesis).
So when the value of alpha is taken as 1% the probability of committing type II error is reduced.
Part D
Increasing sample size makes the hypothesis test more sensitive - more likely to reject the null hypothesis when it is, in fact, false. Thus, it increases the power of the test.
So when sample size is increased to 1000 employees the probability of committing type II error is reduced further.