Question

A large company is being sued for gender discrimination because 20% of newly hired candidates are women when 40% of all applicants were women. You plan to use hypothesis testing to determine whether there is significant evidence that the company's hiring practices are discriminatory. Part A: State the null and alternative hypotheses for the significance test. (2 points) Part B: In the context of the problem, what would a Type I error be? A Type II error? (2 points) Part C: If the hypothesis is tested at a 1% level of significance instead of 5%, how will this affect the power of the test? (3 points) Part D: If the hypothesis is tested based on the hiring of 1,000 employees rather than 100 employees, how will this affect the power of the test? (3 points)

Answer 1

In regards to what the other guy wrote:

For part C) decreasing the significance will reduce the power of the test and increase the probability of committing a type II error. However it will decrease the probability of a type I error.

Explanation:

Type I errors are directly related to significance levels or alpha. Increasing the significance level increases the probability of type I.

Type II errors are inversely related to significance levels. Increasing the significance level will decrease the probability of a type II.

There are many things, like sample size and variance, that will affect the probability of a type II error occurring. So type I error increasing/decreasing does not guarantee that type II will change in the opposite direction 100% of the time (though it is a good rule of thumb that when the probability of one error goes up the other goes down).

Answer 2

Part a:

The hypothesis are
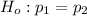`H_o: p_1=p_2` and
`H_a: p_1<p_2`.

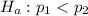Part b:

The Type I error is when the null hypothesis is true but is rejected wrongly. In this case this would indicate that there was no discrimination, but it was wrongly rejected and thus the company is defamed for gender discrimination.

Type II error is when a false null hypothesis is accepted. In this case this would mean that there was a discrimination in the process of hiring but the company is not made accountable for the issue.

Part c:

When the value of alpha is taken as 1% the probability of committing type II error is reduced.

Part d:

When sample size is increased to 1000 employees the probability of committing type II error is reduced further.

Explanation:

As the probability of the women being employed is given as p1 and the probability of the man being employed is given as p2.

Part A

The hypotheses are as follows

The null hypothesis indicate that there is no difference between the probabilities of woman being employed or man being employed. So

`H_o: p_1=p_2`

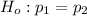
The alternative hypothesis describes that the probability of women employment is less than that of men being employed thus

`H_a: p_1<p_2`

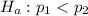
Part B

The Type I error is when the null hypothesis is true but is rejected wrongly. In this case this would indicate that there was no discrimination, but it was wrongly rejected and thus the company is defamed for gender discrimination.

Type II error is when a false null hypothesis is accepted. In this case this would mean that there was a discrimination in the process of hiring but the company is not made accountable for the issue.

Part C

Higher values of α make it easier to reject the null hypothesis, so choosing higher values for α can reduce the probability of a Type II error.

The consequence here is that if the null hypothesis is true, increasing α makes it more likely that we commit a Type I error (rejecting a true null hypothesis).

So when the value of alpha is taken as 1% the probability of committing type II error is reduced.

Part D

Increasing sample size makes the hypothesis test more sensitive - more likely to reject the null hypothesis when it is, in fact, false. Thus, it increases the power of the test.

So when sample size is increased to 1000 employees the probability of committing type II error is reduced further.