Question

Which expression is equivalent to RootIndex 3 StartRoot 32 x Superscript 8 Baseline y Superscript 10 Baseline EndRoot?

Answer 1

C

Explanation:

The Answer is C on Edge.

Answer 2

The equivalent expression to the given expression is
`\sqrt[3]{32x^8y^(10)}=2x^2y^3\sqrt[3]{4x^2y}`

Explanation:

The given expression is
`\sqrt[3]{32x^8y^(10)}`

To find the equivalent expression:

`\sqrt[3]{32x^8y^(10)}=(32x^8y^(10))^{(1)/(3)}`

We may write the above expression as below:

`=(32^{(1)/(3)})((x^8)^{(1)/(3)})((y^(10))^{(1)/(3)})`

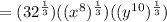
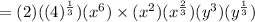`=(2)((4)^{(1)/(3)})(x^6)* (x^2)(x^{(2)/(3)})(y^3)(y^{(1)/(3)})` (using square root properties)

`=(2\sqrt[3]{4})(x^2\sqrt[3]{x^2})(y^3\sqrt[3]{y})` (combining the like terms and doing multiplication )

`=2x^2y^3\sqrt[3]{4x^2y}`

Therefore
`\sqrt[3]{32x^8y^(10)}=2x^2y^3\sqrt[3]{4x^2y}`

Therefore the equivalent expression to the given expression is
`\sqrt[3]{32x^8y^(10)}=2x^2y^3\sqrt[3]{4x^2y}`