Answer:
The equivalent expression to the given expression is
![\sqrt[3]{32x^8y^(10)}=2x^2y^3\sqrt[3]{4x^2y}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/95wbovwn1tmq1mjgfo5983rl3gg8ahd3xi.png)
Explanation:
The given expression is
![\sqrt[3]{32x^8y^(10)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ov1y4xjgwsx55injmj1npadkus3klo57wo.png)
To find the equivalent expression:
![\sqrt[3]{32x^8y^(10)}=(32x^8y^(10))^{(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/fcubuf9fgyfq1gjgdh255vujxt1ql4gjay.png)
We may write the above expression as below:
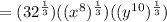
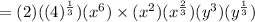 (using square root properties)
(using square root properties)
![=(2\sqrt[3]{4})(x^2\sqrt[3]{x^2})(y^3\sqrt[3]{y})](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ruy7qepy6qtwveops0lhi1f76hc3juw8dx.png) (combining the like terms and doing multiplication )
(combining the like terms and doing multiplication )
![=2x^2y^3\sqrt[3]{4x^2y}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/von9qpalk8a6r0hbzui940c8ykpimweq48.png)
Therefore
![\sqrt[3]{32x^8y^(10)}=2x^2y^3\sqrt[3]{4x^2y}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/95wbovwn1tmq1mjgfo5983rl3gg8ahd3xi.png)
Therefore the equivalent expression to the given expression is
![\sqrt[3]{32x^8y^(10)}=2x^2y^3\sqrt[3]{4x^2y}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/95wbovwn1tmq1mjgfo5983rl3gg8ahd3xi.png)