Answer: A: 0.0031
Explanation:
Given : In a study of wait times at an amusement park, the most popular roller coaster has a mean wait time of 17.4 minutes with a standard deviation of 5.2 minutes.
i.e.
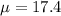 and
and
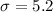
We assume that the wait times are normally distributed.
samples size : n= 30
Let x denotes the sample mean wait time.
Then, the probability that the mean wait time is greater than 20 minutes will be :
![P(x>20)=1-P(x\leq20)\\\\=1-P((x-\mu)/((\sigma)/(√(n)))\leq(20-17.4)/((5.2)/(√(30))))\\\\=1-P(z\leq2.74)\ \ [\because\ z=(x-\mu)/((\sigma)/(√(n)))]\\\\=1-0.9969\ \ [\text{ By z table}]\\\\=0.0031](https://img.qammunity.org/2021/formulas/mathematics/middle-school/le687x2sewk0vgywk9sn3mwaohxc14ifke.png)
Hence, the probability that the mean wait time is greater than 20 minutes.= 0.0031
Thus , the correct answer is A: 0.0031 .