Answer:
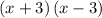
Explanation:
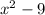
To factor an integer, we need to divide it by the ascending sequence of primes (2, 3, 5). The number of times each prime divides the original integer becomes its exponent.

Now, we need to factor this expression by applying the difference of two squares rule:
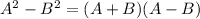
A= x and B= 3
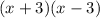
OAmalOHopeO