Question

Which transformations could be performed to show that △ABC is similar to △A"B"C"?

a reflection over the x-axis, then a dilation by a scale factor of 3
a reflection over the x-axis, then a dilation by a scale factor of One-third
a 180° rotation about the origin, then a dilation by a scale factor of 3
a 180° rotation about the origin, then a dilation by a scale factor of One-third

Answer 1

D

Explanation:

Answer 2

A 180° rotation of then a dilation by a scale factor of one-third

Explanation:

The coordinates of the vertices of ΔABC are;

A(-9, 3), B(-9, 6), and C(0, 3)

The coordinates of the vertices of ΔA'B'C' are;

A'(3, -1), B'(3, -2), and C'(0, -1)

We note that for a 180° rotation transformation about the origin, we get;

Coordinates of preimage = (x, y)

Coordinates of image after 180° rotation about the origin = (-x, -y)

Therefore, a 180° rotation of ΔABC about the origin, would give ΔA''B''C'' as follows;

A(-9, 3), B(-9, 6), and C(0, 3) = A''(9, -3), B''(9, -6), and C''(0, -3)

The formula for a dilation of a point about the origin is given as follows;

`D_(O, \, k) (x, \, y) = (k\cdot x, \, k\cdot y)`

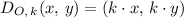
Where;

k =The scale factor = 1/3, (one-third) we have;

A dilation of ΔA''B''C'', by a scale factor of 1/3, we get ΔA'B'C' as follows;

`D_{O, \, (1)/(3) } A''(9, \, -3) = A'((1)/(3) * 9, \, (1)/(3) * -3) = A'(3, -1)`

`D_{O, \, (1)/(3) } B''(9, \, -6) = B'((1)/(3) * 9, \, (1)/(3) * -6) = A'(3, -2)`

`D_{O, \, (1)/(3) } C''(0, \, -3) = C'((1)/(3) * 0, \, (1)/(3) * -3) = C'(0, -1)`

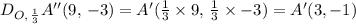
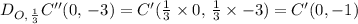
The coordinates of the vertices of ΔA'B'C' are A'(3, -1), B'(3, -2), and C'(0, -1), which is the same as the required coordinates of the image;

Therefore, the transformation that can be performed to show that ΔABC and ΔA'B'C' are similar are rotating ΔABC by 180° then a dilating the image derived after rotation by a scale factor of one-third (1/3) we get ΔA'B'C'.