Answer:
A 180° rotation of then a dilation by a scale factor of one-third
Explanation:
The coordinates of the vertices of ΔABC are;
A(-9, 3), B(-9, 6), and C(0, 3)
The coordinates of the vertices of ΔA'B'C' are;
A'(3, -1), B'(3, -2), and C'(0, -1)
We note that for a 180° rotation transformation about the origin, we get;
Coordinates of preimage = (x, y)
Coordinates of image after 180° rotation about the origin = (-x, -y)
Therefore, a 180° rotation of ΔABC about the origin, would give ΔA''B''C'' as follows;
A(-9, 3), B(-9, 6), and C(0, 3) = A''(9, -3), B''(9, -6), and C''(0, -3)
The formula for a dilation of a point about the origin is given as follows;
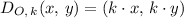
Where;
k =The scale factor = 1/3, (one-third) we have;
A dilation of ΔA''B''C'', by a scale factor of 1/3, we get ΔA'B'C' as follows;
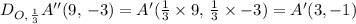
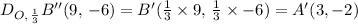
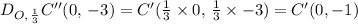
The coordinates of the vertices of ΔA'B'C' are A'(3, -1), B'(3, -2), and C'(0, -1), which is the same as the required coordinates of the image;
Therefore, the transformation that can be performed to show that ΔABC and ΔA'B'C' are similar are rotating ΔABC by 180° then a dilating the image derived after rotation by a scale factor of one-third (1/3) we get ΔA'B'C'.