Answer:
It will take about 10.5 years for the investment to reach $3,300.
Explanation:
Continuous compound is given by:
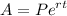
Where P is the principal, e is Euler's number, r is the rate, and t is the time (in this case in years).
Since our principal is $2,000 at a rate of 4.75% or 0.0475, our equation is:
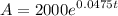
We want to find the number of years it will take for our investment to reach $3,300. So, substitute 3300 for A and solve for t:
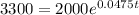
Divide both sides by 2000:
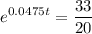
We can take the natural log of both sides:
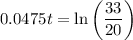
Therefore:
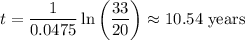
It will take about 10.5 years for the investment to reach $3,300.