Question

How many years will it take $2,000 to grow to $3,300 if it is invested at 4.75% compounded​ continuously?

Answer 1

10.54263764

Explanation:

`3300=2000e^(.0475t)\\\\1.65=e^(.0475t)\\\ln(1.65)=.0475t\\.500775288=.0475t\\t=10.54263764`

Answer 2

It will take about 10.5 years for the investment to reach $3,300.

Explanation:

Continuous compound is given by:

`\displaystyle A=Pe^(rt)`

Where P is the principal, e is Euler's number, r is the rate, and t is the time (in this case in years).

Since our principal is $2,000 at a rate of 4.75% or 0.0475, our equation is:

`\displaystyle A=2000e^(0.0475t)`

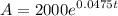
We want to find the number of years it will take for our investment to reach $3,300. So, substitute 3300 for A and solve for t:

`3300=2000e^(0.0475t)`

Divide both sides by 2000:

`\displaystyle e^(0.0475t)=(33)/(20)`

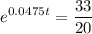
We can take the natural log of both sides:

`\displaystyle 0.0475t=\ln\left((33)/(20)\right)`

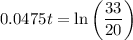
Therefore:

`\displaystyle t=(1)/(0.0475)\ln\left((33)/(20)\right)\approx 10.54\text{ years}`

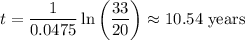
It will take about 10.5 years for the investment to reach $3,300.