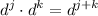Answer:
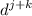
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
- Exponential Rule [Multiplying]:
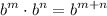
Explanation:
Step 1: Define
Identify
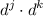
Step 2: Find
- Multiply [Exponential Rule - Multiplying]: