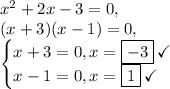Question

0=x^(2)+2x-3 Solve using Quadratic Formula

Answer 1

`x=1,\\x=-3`

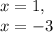
Explanation:

The quadratic formula is given by
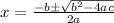`x=(-b\pm√(b^2-4ac))/(2a)`, where
`x` represents both real and nonreal solutions to a quadratic in standard form
`ax^2+bx+c`.

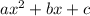Thus, with the given quadratic
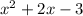`x^2+2x-3`, we can assign values:

• 
  `a=1`
• 
  `b=2`
• 
  `c=-3`

Substituting in these values to the quadratic formula, we have:

`x=(-2\pm√(2^2-4(1)(-3)))/(2(1)), \\\\x=(-2\pm√(16))/(2),\\\\x=(-2\pm 4)/(2),\\\\\begin{cases}x=(-2+4)/(2),x=(2)/(2)=\boxed{1}\\x=(-2-4)/(2),x=(-6)/(2)=\boxed{-3}\end{cases}`

Verify by factoring:

`x^2+2x-3=0,\\(x+3)(x-1)=0,\\\begin{cases}x+3=0,x=\boxed{-3}\:\checkmark\\x-1=0,x=\boxed{1}\:\checkmark\end{cases}`

Answer 2

Explanation:

x^2 + 2x - 3 =0

x^2 + 3x - x -3 = 0

(x) x (x+3) - (x + 3) = 0

(x+3) x (x-1) = 0

x+3=0

x-1=0

x=-3

x=3

x1 =-3, x2 = 1