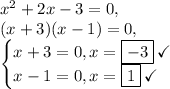Answer:
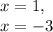
Explanation:
The quadratic formula is given by
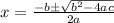 , where
, where
 represents both real and nonreal solutions to a quadratic in standard form
represents both real and nonreal solutions to a quadratic in standard form
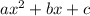 .
.
Thus, with the given quadratic
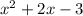 , we can assign values:
, we can assign values:
Substituting in these values to the quadratic formula, we have:
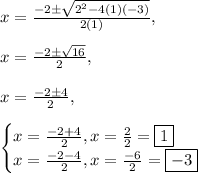
Verify by factoring: