Answer:
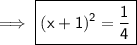
Explanation:
Given :-
- A equation is given to us
- The equation is 4x² + 8x + 3 = 0
And we need to write the equation by completing the square. Here's the step by step explanation .
Step 1: Make the coefficient of x² as 1 :-

Step 2: Rewrite the equation :-
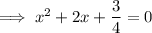
Step 3: Add 1² to both sides :-

Step 4: Rewriting in whole square form:-

Step 5: Simplify the RHS :-
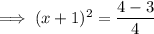
Step 6: The required form of equⁿ :-
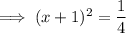
Hence the equation by rewriting it by completing the square is ( x + 1)² = 1/4 .