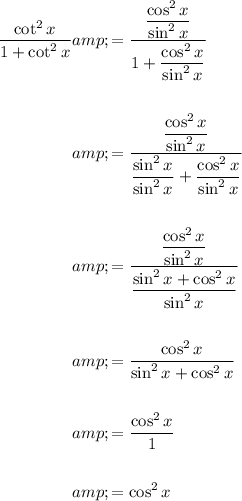Answer:
See below.
Explanation:

Given expression:
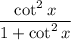
Rewrite cot²x using the trigonometric identity:
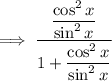
Rewrite the denominator so that is one fraction:
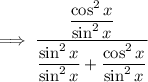
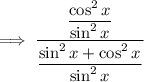

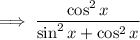
Use the trigonometric identity sin²x + cos²x = 1 :
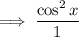
Simplify:
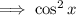
-------------------------------------------------------------------------------------
As one calculation: