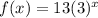Answer:
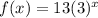
Explanation:

The y-intercept of a function is the y-value when x = 0.
From inspection of the table, the y = 13 when x = 0, so a = 13:
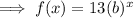
Substitute the ordered pair (1, 39) into the equation and solve for b:
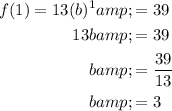
Therefore, the equation for the given table is: