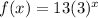Question

Write an equation for the table below:f(x)=a(b)^x

Answer 1

`f(x)=13(3)^x`

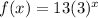
Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

The y-intercept of a function is the y-value when x = 0.

From inspection of the table, the y = 13 when x = 0, so a = 13:

`\implies f(x)=13(b)^x`

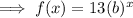
Substitute the ordered pair (1, 39) into the equation and solve for b:

`\begin{aligned}f(1)=13(b)^1&=39\\13b&=39\\b&=(39)/(13)\\b&=3\end{aligned}`

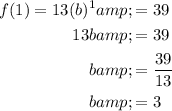
Therefore, the equation for the given table is:

`f(x)=13(3)^x`

Answer 2

f(x) = 13
`(3)^(x)`

Explanation:

we require to find a and b

using ordered pairs from the table and substituting into f(x)

f(x) = a
`(b)^x}`

using (0, 13 )

13 = a
`b^(0)` [
`b^(0)` = 1 ] , then

a = 13

f(x) = 13
`(b)^(x)`

using (1, 39 )

39 = 13
`b^(1)` = 13b ( divide both sides by 13 )

3 = b

f(x) = 13
`(3)^(x)`