The question gives us an absolute value problem.
In order to solve the problem, we should first deal with the 3 by adding 3 to both sides so as to get the absolute value alone and apply a theorem about absolute values which will help us solve the problem.
Let us do this below:
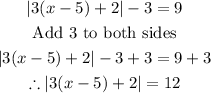
Now that we have the absolute value all alone, let us apply the theorem.
The theorem states:
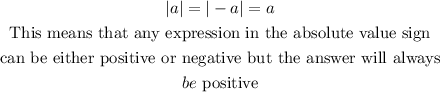
From the explanation, it is clear that there are two possible values for x because:
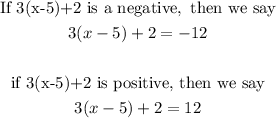
This is because if we place either 12 or -12 into the absolute value, the final answer will be 12
Therefore, let us now solve the resulting 2 equations separately and find the possible values
for x.
This is done below:

This gives the first possible value of x. i.e. x = 25/3
The next possible value of x is gotten by making the same expression equal to -12.

The second possible value of x is 1/3